The Commutative Property Of Addition Is Visually Obvious With Base Ten Blocks
 More time on the blocks, less time on the properties unless you are a teacher. This is a visually obvious property. "Goes with saying". You can SEE it just looking at the tray.
More time on the blocks, less time on the properties unless you are a teacher. This is a visually obvious property. "Goes with saying". You can SEE it just looking at the tray.2 + 1 = 1 + 2
1 + 9 = 9 +1
etc
The Commutative Property Of Addition is perhaps the easiest of the math concepts to explain of all.
1 plus 2 is the same as 2 plus 1. It doesn't matter what order you add them in, they are the same. This comes up in talks about order of operation. PEMDAS.
Which do you add first?
Doesn't matter...just make sure you do everything but subtraction first...
Playing with blocks makes this abundantly clear. It is also why this method has such great success with dyslexic learners. Backwards or forwards 3 + 7 = 7 + 3 when you are looking at blocks, with the symbols not so much.
Base ten blocks make math easy.
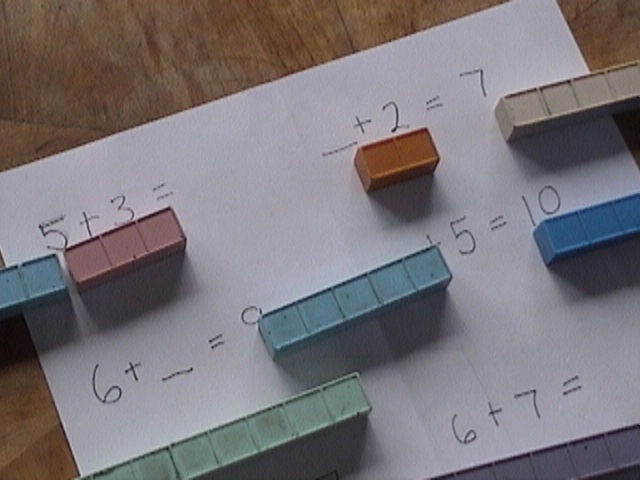 Base ten blocks make basic math concepts visually and blatantly obvious.
Base ten blocks make basic math concepts visually and blatantly obvious.Get you hands on the blocks. Especially with the younger students.
Spend less time fooling with the definitions and more time fooling with the blocks.
DO addition.
"More time doing, less time talking," as they say.

Go from Commutative Property Of Addition back HOME.
“Math illiteracy strikes 8 out of 5 people.”
“The whole is more than the sum of the parts.” Aristotle (384-322 BC)
The Associative Property of Addition.
Distributive Property Of Multiplication
Amazing Addends
The Four Properties of Addition
There are four properties of addition: they are the commutative, associative, additive identity and distributive properties.
Commutative property: When two numbers are added, the sum is the same regardless of the order of the addends.
For example 3 + 2 = 2 + 3 Algebraic: x + y = y + x
Associative Property: When three or more numbers are added, the sum is the same regardless of the order of addition.
The property states that for all real numbers a, b, and c, their sum is always the same, regardless of their grouping:
(a + b) + c = a + (b + c)
For example (1 + 2) + 3 = 1 + (2 + 3) Algebraic: (x + y) + z = x + (y + z)
Additive Identity Property: The sum of any number and zero is the original number.
For example 1 + 0 = 5. Algebraic: x + 0 = x (Crucially important concept especially when you understand 0 = x - x. Hero zero! Helps solve equalities.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number.
For example 4(6 + 3) = (4)(6) + (4)(3)
Algebraic: x(y + z) = xy + xz
Four-year-old math enrichment.
Blog: Addends Towers

Lifetime Passwords are just that...you get a pass for a lifetime. Pay once and you are good, forever. Come back as often as you like. Watch vids, download PDFs. You get all my passwords to get through all my pay walls all for one low price...currently 4 passwords open almost all of my pages.. When you purchase the LIFETIME PASSPORT you get them all for one low price: $999.00...if you want the Algebra course it is $600.00 by itself but only $250.00 with a lifetime Passport. Teacher training is $400.00 but you can break it up into 12 easy installments of 37.00 Or get all four passwords for a few dollars more but 24 months.
Or you can purchase individual modules, & get a lifetime of access. Hit the Contact Us tab for the PayPal link or use the handy buttons provided.
***Unlimited Lifetime Access:
M0AR Training
M0AR Training $100.00
You are guided through two--one hour Introductions, one for "students" and one for "teachers", The Crash Course, Hurricane and Winter training. You can take the cost of is training off any other password or the passport.
Passport: 4 Passwords + AC = All four passwords plus the Algebra Course. Basically all of my passwords for a one time fee of $1249.00. You will also get M0AR Training: the crash course and Hurricane Training + Winter Training and all of my books. Plus you two training passwords, for a total of seven passwords that get you into dozens of pages.
Passport 4 Passwords $999.00 = All four passwords. You will also get the crash course and Hurricane Training and all of my books. But no Algebra Course. You can always buy it separately for $250.00 when you buy all four passwords.
MOD 1: Series A+ Easy PZ + PDFs
PDF Only (MOD I) $100.00 = Module One. PDFs and Books and more PDFs. You get the series A manuals, my books and the EZ PZ Overview. You will also get the Crash Course and Hurricane Training. This module has all ten Series A Manuals online plus my books and workbooks, as well as worksheets for learning how to write numbers, pdfs explaining the method and make it EZ PZ, pdfs for practicing concepts. A plethora of PDFs all in on place. Most of them have explanatory videos to go along with them so you get best use out of them. It will take you quite a while to download and print it all. This has an entry page.
MOD 2: Parent Teacher Training + M0AR Training
Training (MOD II) $400.00 = Module Two. Training you won't get anywhere else. You will also get the Crash Course, Hurricane Training, and Winter Training, plus all of my books. Module one and two are a great combination. You will learn how to teach math using base ten blocks whether you are planning to homeschool or a side hustle, this Module will put you well ahead of any competition. Best of all the videos are fun...they may not be exactly entertaining, but they certainly are engaging. i get great results so you will get great results because i teach you how and the theory behind it, in other words how and WHY. This page has an entry page.
MOD 3 : Sitewide + PDFs
SiteWide (MOD III) $250.00 = Module Three is the most bang for your buck. It isn't so much a module with an entry page as a collection of pages. When in doubt try the Mod III password. Coupled with Module One, you basically get my website from years ago before i added all the parent/teacher training and the so called "advanced" pages. Spend time on these pages and training will be a breeze. Module Three puts theory into practice. Example IS the lesson. Module Two gives you theory and some practice, this module is all theory IN practice right in front of your eyes, you see and hear the children learning in real time. You can hear the ah-ha moments...the lessons are unrehearsed with real students. They are fun because learning is fun and watching others learn is fun too. This is in and of itself is priceless training.
MOD 4: "Advanced Pages" + Allegedly Advanced Algebra
"Advanced" (Module IV) $250.00 = i say "advanced" because Module Four is higher level math, but really you are still just creatively applying the five basic concepts. Not to mention you'll see 7 year olds doing it and showing you how to do it too. It has however come to my attention that other curriculums are not using the blocks to teach upper level algebra, and resort to symbols only in their books. i put the pictures back in and show you what the symbols mean and what the problems look like. This greatly enhances speed and efficiency of learning as well as making abstract concepts accessible to kinesthetic learners who can build the problems from the drawings. Visual learners love this method because they can see the symbols and operations, which makes it fun.
i have lots of explanatory videos to make and add. i also have several entry or landing pages to build. When the dust settles it should be much easier to navigate, to get started, & to know what to do next.
Algebra Course
$600.00. $250.00 with $999.00 PassPort.
Prerequisites: The ability to count to nine. Identify if something is same or different or not. Be able to identify a rectangle or square.
Now with Module IV. When you buy the algebra course you get module four too. Between these two passwords algebra will be a cinch.
i use base ten blocks to teach ALL topics. i don't resort to symbol only lessons until AFTER we have played with blocks. Get your blocks paper and pencil and play along, my success rate with people who have failed algebra or struggled in college is 100%. If you require more explanation or assistance email me, this password comes with tech support, we will set up 1 hour video chat. i usually clear up any confusion in under 15 minutes.
Course covers:
Pre Algebra:
Integers
Number line
Algebra:
Factoring polynomials.
Completing the square.
Square numbers.
Radicals.
Graphing y = mx+b
Graphing polynomials.
Vertex Form.
Basic Trig Functions.
Problem solving.
System of equations.
Derivation Of The Quadratic Equation.
+ more.
Lessons last about 1 hour to 90 minutes (max) each. These are recordings of actual tutoring sessions that cost the parent $250.00 per 5 lessons or over $1500.00 (not all the lessons got recorded and put here). You can watch them for $25 per lesson (half off) or get the whole course for a one time payment of $600.00 Here is more than 30 hours of Algebra instruction using base ten blocks you won't get anywhere else.
As it turns out, people who i thought were using base ten blocks to teach algebra AREN'T.
https://www.crewtonramoneshouseofmath.com/Algebra-with-base-10-blocks.html
Bonus Lesson:
Playing while learning basic math concepts.


